This is the continuation of an older series of posts on model rocket stability for beginners - rocket n00bs. Click here to return to Part 1, and here for Part 2.
In the previous posts on model rocket stability, we talked about Center of Gravity (CG) and Center of Pressure (CP) on a rocket, and where the two should be in relation to one another (CG ahead of CP). We learned that the purpose of fins is twofold: to move the CP aftward - behind the CG - and to correct a rocket's trajectory and dampen the back-and-forth oscillation you naturally get in rocket flight through the air.
But how do we know where the Center of Pressure is? How far behind the Center of Gravity should it be - can the CP be too close or too far from the CG? And what can we do to fix an unstable or understable rocket?
We're going to devote the next few posts to different ways of finding the Center of Pressure, then move on to other questions on stability. This is exciting stuff, because once you understand the basics of model rocket stability, you can do some interesting things. You can design and build your own rockets, knowing they'll fly safely. Even if you mainly prefer to build kits, understanding stability will enable you to modify those kits - such as building them to fly with larger, more powerful motors, or converting single-stage rockets to high-flying multistage rockets by adding a booster section.
 |
| An upcoming project - an Estes Photon Probe* kit with a booster - now a two-stage rocket! |
* * *
First, finding the Center of Gravity - also known as the Center of Mass - is simple enough. All you have to do is balance the rocket on its side. You can do this on a finger, the back of a chair, or the edge of a ruler (if you can get it to stay still). I like to use a piece of string with a loop tied in the end. Balancing a model rocket on a chair back, which I have done, you run the risk of it falling off and breaking. With a string, I don't worry about the rocket falling to the floor.
When locating the CG for checking stability, it's important to have the rocket prepped to fly. In other words, you need to install a motor, recovery wadding, and the parachute.
Once you've located the point where the rocket balances without tipping one way or another, you've found the Center of Gravity. The CG is the rocket's balance point, and as it flies, the rocket will rotate back and forth around this point as the fins keep the rocket pointed upward.
 |
| Finding the CG on an Apogee Avion rocket |
Once you've located the point where the rocket balances without tipping one way or another, you've found the Center of Gravity. The CG is the rocket's balance point, and as it flies, the rocket will rotate back and forth around this point as the fins keep the rocket pointed upward.
Well, the Center of Pressure is another kind of balance point, but rather than being a balance point of all the mass or weight of the parts of the rocket, it's an aerodynamic balance point. It's the theoretical point on the rocket where the sum of all the aerodynamic pressure is in balance. It has to do with surface area rather than the relative weight of the rocket's parts.
So, while a heavier nose cone might change the CG, its weight has no bearing on the CP. It has to do with the shapes and sizes of all the external parts of the rocket. How on earth do you figure out where that point is?
So, while a heavier nose cone might change the CG, its weight has no bearing on the CP. It has to do with the shapes and sizes of all the external parts of the rocket. How on earth do you figure out where that point is?
That question plagued rocketeers in the early days of model rocketry. They knew what the CP was, and knew it had to be behind the CG, but how were you supposed to know where the CP would be on a given rocket design?
There are three basic methods. Today, we'll look at the earliest and most basic one.
The Cutout Method
 |
| From Estes' The Classic Collection |
In the early days of model rocketry, people knew that the CP had to do with surface area, and needed to find a simple way of locating the center of the surface area of their rockets. Specifically, the center of lateral area - the center of the area of the rocket as viewed from the side. It would be easy to find the center of area looking at the rocket from straight on - it's the tip of the nose cone.
How do you find the center of lateral area of a 3-dimensional rocket-shaped object? The answer is to simplify things a bit.
It's actually simple to find the center of area of an oddly-shaped two-dimensional object. You balance it. If we had a two-dimensional representation of our rocket, we could find its geometric center or centroid.
 |
| Using the plumb line method to find the centroid of an odd shape |
The cutout method involved making an accurate drawing of a rocket on a stiff material such as card stock or cardboard, cutting the drawing out, and balancing it. Since the card stock is of uniform thickness and density throughout, its Center of Gravity and Center of Area are the same thing!
Here's a cutout of a simple model rocket - Sounder IB - balanced on a piece of aluminum angle.
Here's a cutout of a simple model rocket - Sounder IB - balanced on a piece of aluminum angle.
Once we've found the center of lateral area for our rocket design, we know that as wind hits that object, it should be balanced at the geometric center. Because the air pressure would be equal on all sides of that point, that's our CP. If you were to balance the rocket at that point and hold it in the fast moving air of a fan, you could point the rocket sideways, but it wouldn't pivot - the air pressure would be equal in front of and behind the CP.
As long as when we build the rocket, we make sure that the CG is ahead of that point, we should have a stable rocket.
 |
| From Centuri technical report TIR-30, by James Barrowman |
Of course, the cutout method has some drawbacks, a couple of which can be deduced from the photo above.
The first is that it requires that you be able to draw an accurate representation of your rocket design, with all parts correctly proportional and in exactly the place they will be on the finished model. Not everyone is terribly gifted at drawing these days, so you'd have to be able to draft an accurate design with tools - rulers, curves, maybe a compass, etc. (Since am not skilled at drafting, I used a printout from an OpenRocket design just to show you the cutout method above. And since I have OpenRocket, I really don't need to use the cutout method - but I wanted to show it, and since I can't draw, I cheated here.)
Another drawback is this: Drawing a two-dimensional representation of your three-dimensional rocket may not tell the whole story. A rocket seen only in silhouette is not the same as the real, 3D thing.
As an illustration, here are three very similar - but significantly different - model rocket designs.
Sounder IB is a four-finned rocket, so it's simple to create a symmetrical, reasonably accurate drawing of it.
The three rockets above - which I haven't named - are all the same design. They have 18-inch long body tubes, a 4-inch plastic nose cone, and trapezoidal fins. The only difference is the number of fins - three, four, and eight.
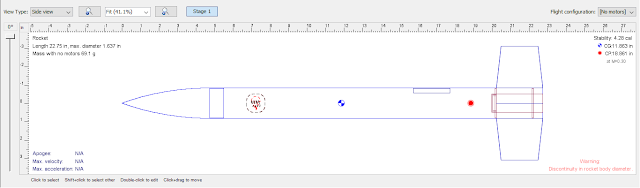
Let's start with the four-finned rocket, since that's symmetrical in multiple directions. Here's what the drawing we would make of it on cardboard would be shaped like.
Pretty simple.
For the moment, ignore the blue and white CG marking and the red and white CP marking. We'll get to those in a bit. Also, ignore that I've done this drawing using model rocket design software. Let's pretend - just for now - that we're looking at a good drawing done by hand.
If we cut out along all the lines of our drawing, we can see that the end of our two-dimensional cardboard cutout with the fins on it will be heavier, and that the CP of the rocket will be closer to that end than to the nose cone end. As we look at the design, we see two of the fins directly from the side - in other words, we can see their full outline straight on.
Of course, if we turn the rocket 45 degrees, then our two-dimensional drawing looks a little bit different.
The fins of the rocket are the same size as they were before, but in our two-dimensional representation, they look smaller. That means that, if we were to use this drawing to find our CP, it would seem like it was further forward than if we used the first drawing. But, of course, the actual CP on the rocket isn't dependent on which way you look at the rocket.
Of course, most likely nobody would have drawn their rocket like this to find the CP, so this might seem a bit silly. But it does begin to give an idea of the limitations of the cutout method.
So, let's look at a three-finned model.
Now, with this drawing, we're looking at two of three fins, which would be 120 degrees apart on a rocket. Since we're seeing one fin directly face on, we're seeing another one at an angle, and so in this drawing, the fins are lopsided. That's OK, of course, because we're not trying to balance our cutout along the rocket's vertical axis - from nose tip through the motor nozzle. And, of course, we could rotate the view of the rocket by 30 degrees and see it like this:
Now we're seeing two fins at an angle, so they're smaller than they would look face on. The third fin is on the opposite side of the rocket, pointed directly away from us.
Because the fins in this drawing look smaller, a cutout of this balanced on a ruler would indicate that the CP is further forward than on the four-finned rocket - which would be correct. If you add more fins, there is more surface area on the back of the rocket, and the CP moves aftward.
So, which way should you draw your rocket if it has three fins? Well, it might not matter. Perhaps you'd find that both drawings have the same area, and the balance point of the cutout would be the same. But, in fact, I've found no explicit instructions about what to do for a three-finned rocket when using the cutout method. Again, either one will work, and if you build your rocket with the CG forward where the balance point is on the two-dimensional cutout, the rocket will be stable.
Since we've established that adding more fins moves the CP toward the rear of the rocket, let's go in the opposite direction. Instead of three or four fins, let's build a rocket with eight.
If you draw a two-dimensional outline of the four-finned rocket seen above, you get this:
Because you're creating a two-dimensional outline of this rocket, the four-finned version and the eight-finned version look exactly the same, which means that the cutout method suggests that these two rockets have the same Center of Pressure, despite one having twice the fins of the other!
Now, of course, you may well already know that, in OpenRocket or RockSim, the Center of Pressure is indicated by the red circle with the red dot in the middle, seen above in all the designs. And the CP on the cutout of Sounder is far behind the spot where it is balancing on the aluminum angle.
You probably also know that the CG is indicated with the blue and white checkerboard circle. The CG in these designs is an estimate, calculated based on what I've told the software each of the component parts weighs. You'll notice that, regardless of what the rocket looks like in silhouette, as I add more fins, the CP moves aftward.
You can see that all of these rocket designs have the CG well ahead of the CP, and are stable. That includes Sounder - even though the blue CG mark is behind the spot where my cutout balances on the aluminum angle! In order to make Sounder stable, according to the cutout method, it looks like I'd have to make the front end of the rocket much heavier, to move the CG further forward.
So, what gives? Can the cutout method be said to represent the CP of a rocket at all?
Well, the answer is yes - but only in certain circumstances. We'll talk about that in the next post.
Click here for Part 4.
*Original OpenRocket file by Jim Parsons - a.k.a. K'Tesh. His OpenRocket work can be found on The Rocketry Forum in this thread. It's helpful to have these, because you can take them and tweak them, which is a lot of fun.
Follow me on Twitter.
Like my Facebook page for blog updates and extra stuff.
Have a question you'd like to see addressed on this blog? Email me at iamtherocketn00b@gmail.com.
The three rockets above - which I haven't named - are all the same design. They have 18-inch long body tubes, a 4-inch plastic nose cone, and trapezoidal fins. The only difference is the number of fins - three, four, and eight.
Let's start with the four-finned rocket, since that's symmetrical in multiple directions. Here's what the drawing we would make of it on cardboard would be shaped like.
Pretty simple.
For the moment, ignore the blue and white CG marking and the red and white CP marking. We'll get to those in a bit. Also, ignore that I've done this drawing using model rocket design software. Let's pretend - just for now - that we're looking at a good drawing done by hand.
If we cut out along all the lines of our drawing, we can see that the end of our two-dimensional cardboard cutout with the fins on it will be heavier, and that the CP of the rocket will be closer to that end than to the nose cone end. As we look at the design, we see two of the fins directly from the side - in other words, we can see their full outline straight on.
Of course, if we turn the rocket 45 degrees, then our two-dimensional drawing looks a little bit different.
The fins of the rocket are the same size as they were before, but in our two-dimensional representation, they look smaller. That means that, if we were to use this drawing to find our CP, it would seem like it was further forward than if we used the first drawing. But, of course, the actual CP on the rocket isn't dependent on which way you look at the rocket.
Of course, most likely nobody would have drawn their rocket like this to find the CP, so this might seem a bit silly. But it does begin to give an idea of the limitations of the cutout method.
So, let's look at a three-finned model.
Now, with this drawing, we're looking at two of three fins, which would be 120 degrees apart on a rocket. Since we're seeing one fin directly face on, we're seeing another one at an angle, and so in this drawing, the fins are lopsided. That's OK, of course, because we're not trying to balance our cutout along the rocket's vertical axis - from nose tip through the motor nozzle. And, of course, we could rotate the view of the rocket by 30 degrees and see it like this:
Now we're seeing two fins at an angle, so they're smaller than they would look face on. The third fin is on the opposite side of the rocket, pointed directly away from us.
Because the fins in this drawing look smaller, a cutout of this balanced on a ruler would indicate that the CP is further forward than on the four-finned rocket - which would be correct. If you add more fins, there is more surface area on the back of the rocket, and the CP moves aftward.
So, which way should you draw your rocket if it has three fins? Well, it might not matter. Perhaps you'd find that both drawings have the same area, and the balance point of the cutout would be the same. But, in fact, I've found no explicit instructions about what to do for a three-finned rocket when using the cutout method. Again, either one will work, and if you build your rocket with the CG forward where the balance point is on the two-dimensional cutout, the rocket will be stable.
Since we've established that adding more fins moves the CP toward the rear of the rocket, let's go in the opposite direction. Instead of three or four fins, let's build a rocket with eight.
If you draw a two-dimensional outline of the four-finned rocket seen above, you get this:
Because you're creating a two-dimensional outline of this rocket, the four-finned version and the eight-finned version look exactly the same, which means that the cutout method suggests that these two rockets have the same Center of Pressure, despite one having twice the fins of the other!
Now, of course, you may well already know that, in OpenRocket or RockSim, the Center of Pressure is indicated by the red circle with the red dot in the middle, seen above in all the designs. And the CP on the cutout of Sounder is far behind the spot where it is balancing on the aluminum angle.
You probably also know that the CG is indicated with the blue and white checkerboard circle. The CG in these designs is an estimate, calculated based on what I've told the software each of the component parts weighs. You'll notice that, regardless of what the rocket looks like in silhouette, as I add more fins, the CP moves aftward.
You can see that all of these rocket designs have the CG well ahead of the CP, and are stable. That includes Sounder - even though the blue CG mark is behind the spot where my cutout balances on the aluminum angle! In order to make Sounder stable, according to the cutout method, it looks like I'd have to make the front end of the rocket much heavier, to move the CG further forward.
So, what gives? Can the cutout method be said to represent the CP of a rocket at all?
Well, the answer is yes - but only in certain circumstances. We'll talk about that in the next post.
Click here for Part 4.
*Original OpenRocket file by Jim Parsons - a.k.a. K'Tesh. His OpenRocket work can be found on The Rocketry Forum in this thread. It's helpful to have these, because you can take them and tweak them, which is a lot of fun.
Follow me on Twitter.
Like my Facebook page for blog updates and extra stuff.
Have a question you'd like to see addressed on this blog? Email me at iamtherocketn00b@gmail.com.









No comments:
Post a Comment