Stability - or - What Happened to Homer's Rocket? (Part 4) - Finding the CP: Method 1 Continued

This is a continuation of a series on model rocket stability for beginners. Click here to go go the beginning of the series. Click here to read the last post.

Last time, we discussed the earliest method of finding the Center of Pressure (CP) on a model rocket - the cutout method. This simple method ensured stable flights on every model in the early days of model rocketry. Finding the CP is a crucial problem to solve, because in order for stable rocket flight, the CP must be behind the Center of Gravity (CG).

But, of course, the cutout method had drawbacks. Rocketeers had to be reasonably skilled at drawing an accurate representation of the rocket on stiff paper or cardboard, with all the parts in correct proportion. In other words, in order for the cutout method to work the drawing had to look just like the real thing.

Since I'm not a skilled draftsman, I cheated a little. I illustrated the cutout method with a design I'd created in OpenRocket - Sounder IB - which I printed on heavy card stock, cut out, and balanced on a piece of aluminum angle.

This showed us another drawback of the cutout method - accuracy. While balancing the two-dimensional cutout of Sounder IB did find the center of area for the rocket, that point was far forward of the red CP mark on the drawing itself. In other words, OpenRocket told me that the CP was in one spot, but the cutout method indicated that the CP was a good two inches further forward. So far, in fact, that the CP as determined by the cutout method was in front of the CG, as calculated by OpenRocket.

So, while the OpenRocket design showed the rocket to be perfectly stable, the cutout method showed me a dangerously unstable rocket - one which would flip violently around if it were launched!

So, does the cutout method represent the Center of Pressure at all? Or were rocketeers merely fooling themselves? And how do we - how does OpenRocket - know where the CP actually is? Who's right, who's wrong, and why?

The answer is that they're both right - kind of.

In the cutout method, we're balancing a 2D representation of the rocket - on its side. The cutout is resting on its balance point, so as the force of gravity pulls on it, the force is equally distributed in front of and behind the aluminum angle. This force - gravity - is acting a substitute for another force - air pressure - in the real rocket. So, for the cutout method to represent reality, the air pressure would have to be hitting the rocket directly from the side. The cutout method shows you were the CP would be if the rocket were flying sideways!

In this case, that means that all the air is hitting the rocket from the side - at an angle of 90 degrees. The angle the wind is hitting a rocket is known as angle of attack.

Alpha represents the angle of attack. Image from Centuri TIR-30, by James Barrowman.

In The Handbook of Model Rocketry, a 90-degree angle of attack is described as "the worst possible flying condition." In fact, it's an imaginary flying condition, because rockets do not fly sideways. They fly pointy end first!

Under normal flying conditions, with the proper motor (providing enough thrust for the weight of the rocket), model rockets fly at or near zero degrees angle of attack. While the ambient wind tends to blow horizontally along the ground, the rocket flies fast enough upward that the effect of the wind is minimized. If the wind on launch day is, say, 8 miles per hour, and the rocket is flying upward at, say, 200 miles per hour, the rocket will barely notice the wind coming from the side.

Under those conditions, the determination of the Center of Pressure is dominated much more by the fins and nose cone than by the surface area of the body of the rocket. As the rocket wobbles during flight - totally normal for a model rocket - the angle of attack will swing back and forth between zero and a few degrees. As this happens, the fins, which stick out from the body of the rocket, use the oncoming air pressure to correct the rocket's path, causing the back end to rotate away from the wind.

The pressure on the body tube at or near zero degrees angle of attach is much lower, and has much less effect on the CP.

But if the angle of attack were to suddenly increase significantly, then the air pressure on the nose cone and body tube becomes much more significant. The effect is that, at high angle of attack, the Center of Pressure moves forward. If, due to some (imaginary) catastrophic event in flight, the rocket were to fly sideways, then the CP would move forward enough that it would be where we see it when we do the cutout method.

As angle of attack increases, the influence of the nose cone and body tube increase -
the CP moves forward! Image from Centuri TIR-30, by James Barrowman

There are only two situations I know of when a normal rocket experiences these conditions. The first is when the rocket is sitting on the launch pad, and the breeze is blowing across the field. But when the rocket is sitting still on the pad, it's not flying, so this doesn't count.

The other is a rare, pretty strange event, which I've seen twice - recovery.

Once in a while, a rocket will launch, fly to apogee, and then due either to an ejection charge failure or a nose cone which is stuck on too tight, the nose cone doesn't eject. The rocket stays intact, the parachute does not come out, and the rocket begins to fall back to Earth.

Normally, when this happens, it's pretty frightening. Because the rocket is stable, with its CG in front of its CP, it will tend to fly nose first. So a rocket which has an ejection failure usually comes in ballistic - taking a nose dive straight at the ground with increasing speed. This usually destroys the rocket.

Sometimes, very rarely, an odd thing will happen. The rocket will go up, tip over at apogee, and begin falling back down. In rare instances, the CP at 90 degrees angle of attack will be the same spot as the rocket's CG. The rocket is then neutrally stable. The forces of gravity and air pressure are both centered on the same spot. The rocket descends sideways. Since the Center of Gravity is the point of rotation, and the Center of Pressure is the balance point of the force of the air of the rocket, the whole thing is in balance - just like a balanced scale.

If she weighs the same as a duck...

Both times this happened, the rocket fell very slowly, and came to a soft landing. Both times, I was filming, but both times, I was so stunned, I missed getting the slowly descending sideways rocket in frame. But it was pretty cool - and certainly a relief not to have the rocket come in ballistic.

I should mention that you shouldn't try to replicate this, by gluing on a nose cone or something. It's a chance event when it happens, and the same rocket might not do it twice - a slight difference in Center of Gravity could change everything, and the rocket would come in ballistic. But if you do see it, it's kind of amazing.

* * *

The fact that the CP can shift forward is really important. It means that the CG and CP could be too close together for the rocket to remain stable. If the angle of attack suddenly increases, due to a gust of wind, or off-center thrust of the motor, or any number of things, having the CG too close to the CP means that under certain circumstances, the CP could move forward of the CG! If these two switch position, you now have a dangerous, unstable rocket.

This brings us to the question How far forward of the CP chould the CG be? I was going to save this for a later part of this series, but I think it makes sense to mention it here.

In general, the rule of thumb is that the CG should be at least one body tube diameter ahead of the CP. That means that if the rocket is, say, 1 inch in diameter, the CG must be at least 1 inch forward of the CP. This margin is known as caliber, and refers to the diameter of the rocket.

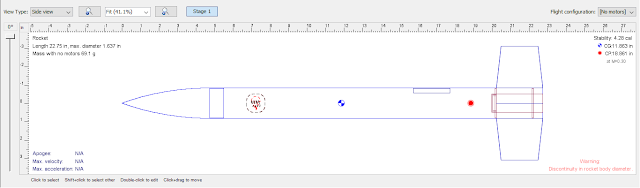
Sounder 1B is 0.976 inches or 24.8 millimeters in diameter. If the CG is exactly 0.976 inches or 24.8 mm ahead of the CP, we say the rocket has a stability margin (sometimes called the static margin) of 1 caliber. If the CG and CP are 1.952 inches or 49.6mm apart - twice the diameter of the body tube - the margin is 2 caliber.

As you see, Sounder 1B has a static margin of 1.63 caliber. The CG is 40 millimeters forward of the CP. Since the minimum static margin is 1 caliber stability, this is fine. The ideal, especially if you want to fly as high as you can, is a static margin between 1 and 2 caliber. More is usually OK, up to a point. Less is generally not enough for safety, except in the case of some short, stubby rockets.

For most model rockets, however, the minimum safe static margin is 1 caliber. Having a static margin of 1 caliber or more ensures that, even if the rocket encounters a high-degree angle of attack for a moment, the CP isn't likely to shift forward of the CG. The rocket should remain stable.

* * *

To be clear, the cutout method does work to make stable rockets. But it's what we could call overly conservative with its CP location. A rocket designed using the cutout method would certainly be stable and safe, but it errs so far on the safe side, that you may end up building rockets which are far heavier in the nose cone than they need to be, or with more fins or larger fins than you need. That means you may rob yourself of performance, or you may shy away from building a rocket which is perfectly safe and stable, because you worry it might not be.

A better, more accurate method of finding the Center of Pressure was called for. We'll discuss that method in the next post.

Click here for Part 5.

Follow me on Twitter.

Like my Facebook page for blog updates and extra stuff.

Have a question you'd like to see addressed on this blog? Email me at iamtherocketn00b@gmail.com.

Stability - or - What Happened to Homer's Rocket? (Part 3) - Finding the CP: Method 1

This is the continuation of an older series of posts on model rocket stability for beginners - rocket n00bs. Click here to return to Part 1, and here for Part 2.

In the previous posts on model rocket stability, we talked about Center of Gravity (CG) and Center of Pressure (CP) on a rocket, and where the two should be in relation to one another (CG ahead of CP). We learned that the purpose of fins is twofold: to move the CP aftward - behind the CG - and to correct a rocket's trajectory and dampen the back-and-forth oscillation you naturally get in rocket flight through the air.

But how do we know where the Center of Pressure is? How far behind the Center of Gravity should it be - can the CP be too close or too far from the CG? And what can we do to fix an unstable or understable rocket?

We're going to devote the next few posts to different ways of finding the Center of Pressure, then move on to other questions on stability. This is exciting stuff, because once you understand the basics of model rocket stability, you can do some interesting things. You can design and build your own rockets, knowing they'll fly safely. Even if you mainly prefer to build kits, understanding stability will enable you to modify those kits - such as building them to fly with larger, more powerful motors, or converting single-stage rockets to high-flying multistage rockets by adding a booster section.

An upcoming project - an Estes Photon Probe* kit with a booster - now a two-stage rocket!

* * *

First, finding the Center of Gravity - also known as the Center of Mass - is simple enough. All you have to do is balance the rocket on its side. You can do this on a finger, the back of a chair, or the edge of a ruler (if you can get it to stay still). I like to use a piece of string with a loop tied in the end. Balancing a model rocket on a chair back, which I have done, you run the risk of it falling off and breaking. With a string, I don't worry about the rocket falling to the floor.

Finding the CG on an Apogee Avion rocket

When locating the CG for checking stability, it's important to have the rocket prepped to fly. In other words, you need to install a motor, recovery wadding, and the parachute.

Once you've located the point where the rocket balances without tipping one way or another, you've found the Center of Gravity. The CG is the rocket's balance point, and as it flies, the rocket will rotate back and forth around this point as the fins keep the rocket pointed upward.

Well, the Center of Pressure is another kind of balance point, but rather than being a balance point of all the mass or weight of the parts of the rocket, it's an aerodynamic balance point. It's the theoretical point on the rocket where the sum of all the aerodynamic pressure is in balance. It has to do with surface area rather than the relative weight of the rocket's parts.

So, while a heavier nose cone might change the CG, its weight has no bearing on the CP. It has to do with the shapes and sizes of all the external parts of the rocket. How on earth do you figure out where that point is?

That question plagued rocketeers in the early days of model rocketry. They knew what the CP was, and knew it had to be behind the CG, but how were you supposed to know where the CP would be on a given rocket design?

There are three basic methods. Today, we'll look at the earliest and most basic one.

The Cutout Method

From Estes' The Classic Collection

In the early days of model rocketry, people knew that the CP had to do with surface area, and needed to find a simple way of locating the center of the surface area of their rockets. Specifically, the center of lateral area - the center of the area of the rocket as viewed from the side. It would be easy to find the center of area looking at the rocket from straight on - it's the tip of the nose cone.

How do you find the center of lateral area of a 3-dimensional rocket-shaped object? The answer is to simplify things a bit.

It's actually simple to find the center of area of an oddly-shaped two-dimensional object. You balance it. If we had a two-dimensional representation of our rocket, we could find its geometric center or centroid.

Using the plumb line method to
find the centroid of an odd shape

The cutout method involved making an accurate drawing of a rocket on a stiff material such as card stock or cardboard, cutting the drawing out, and balancing it. Since the card stock is of uniform thickness and density throughout, its Center of Gravity and Center of Area are the same thing!

Here's a cutout of a simple model rocket - Sounder IB - balanced on a piece of aluminum angle.

Once we've found the center of lateral area for our rocket design, we know that as wind hits that object, it should be balanced at the geometric center. Because the air pressure would be equal on all sides of that point, that's our CP. If you were to balance the rocket at that point and hold it in the fast moving air of a fan, you could point the rocket sideways, but it wouldn't pivot - the air pressure would be equal in front of and behind the CP.

As long as when we build the rocket, we make sure that the CG is ahead of that point, we should have a stable rocket.

From Centuri technical report TIR-30, by James Barrowman

Of course, the cutout method has some drawbacks, a couple of which can be deduced from the photo above.

The first is that it requires that you be able to draw an accurate representation of your rocket design, with all parts correctly proportional and in exactly the place they will be on the finished model. Not everyone is terribly gifted at drawing these days, so you'd have to be able to draft an accurate design with tools - rulers, curves, maybe a compass, etc. (Since am not skilled at drafting, I used a printout from an OpenRocket design just to show you the cutout method above. And since I have OpenRocket, I really don't need to use the cutout method - but I wanted to show it, and since I can't draw, I cheated here.)

Another drawback is this: Drawing a two-dimensional representation of your three-dimensional rocket may not tell the whole story. A rocket seen only in silhouette is not the same as the real, 3D thing.

As an illustration, here are three very similar - but significantly different - model rocket designs.

Sounder IB is a four-finned rocket, so it's simple to create a symmetrical, reasonably accurate drawing of it.

The three rockets above - which I haven't named - are all the same design. They have 18-inch long body tubes, a 4-inch plastic nose cone, and trapezoidal fins. The only difference is the number of fins - three, four, and eight.

Let's start with the four-finned rocket, since that's symmetrical in multiple directions. Here's what the drawing we would make of it on cardboard would be shaped like.

Pretty simple.

For the moment, ignore the blue and white CG marking and the red and white CP marking. We'll get to those in a bit. Also, ignore that I've done this drawing using model rocket design software. Let's pretend - just for now - that we're looking at a good drawing done by hand.

If we cut out along all the lines of our drawing, we can see that the end of our two-dimensional cardboard cutout with the fins on it will be heavier, and that the CP of the rocket will be closer to that end than to the nose cone end. As we look at the design, we see two of the fins directly from the side - in other words, we can see their full outline straight on.

Of course, if we turn the rocket 45 degrees, then our two-dimensional drawing looks a little bit different.

The fins of the rocket are the same size as they were before, but in our two-dimensional representation, they look smaller. That means that, if we were to use this drawing to find our CP, it would seem like it was further forward than if we used the first drawing. But, of course, the actual CP on the rocket isn't dependent on which way you look at the rocket.

Of course, most likely nobody would have drawn their rocket like this to find the CP, so this might seem a bit silly. But it does begin to give an idea of the limitations of the cutout method.

So, let's look at a three-finned model.

Now, with this drawing, we're looking at two of three fins, which would be 120 degrees apart on a rocket. Since we're seeing one fin directly face on, we're seeing another one at an angle, and so in this drawing, the fins are lopsided. That's OK, of course, because we're not trying to balance our cutout along the rocket's vertical axis - from nose tip through the motor nozzle. And, of course, we could rotate the view of the rocket by 30 degrees and see it like this:

Now we're seeing two fins at an angle, so they're smaller than they would look face on. The third fin is on the opposite side of the rocket, pointed directly away from us.

Because the fins in this drawing look smaller, a cutout of this balanced on a ruler would indicate that the CP is further forward than on the four-finned rocket - which would be correct. If you add more fins, there is more surface area on the back of the rocket, and the CP moves aftward.

So, which way should you draw your rocket if it has three fins? Well, it might not matter. Perhaps you'd find that both drawings have the same area, and the balance point of the cutout would be the same. But, in fact, I've found no explicit instructions about what to do for a three-finned rocket when using the cutout method. Again, either one will work, and if you build your rocket with the CG forward where the balance point is on the two-dimensional cutout, the rocket will be stable.

Since we've established that adding more fins moves the CP toward the rear of the rocket, let's go in the opposite direction. Instead of three or four fins, let's build a rocket with eight.

If you draw a two-dimensional outline of the four-finned rocket seen above, you get this:

Because you're creating a two-dimensional outline of this rocket, the four-finned version and the eight-finned version look exactly the same, which means that the cutout method suggests that these two rockets have the same Center of Pressure, despite one having twice the fins of the other!

Now, of course, you may well already know that, in OpenRocket or RockSim, the Center of Pressure is indicated by the red circle with the red dot in the middle, seen above in all the designs. And the CP on the cutout of Sounder is far behind the spot where it is balancing on the aluminum angle.

You probably also know that the CG is indicated with the blue and white checkerboard circle. The CG in these designs is an estimate, calculated based on what I've told the software each of the component parts weighs. You'll notice that, regardless of what the rocket looks like in silhouette, as I add more fins, the CP moves aftward.

You can see that all of these rocket designs have the CG well ahead of the CP, and are stable. That includes Sounder - even though the blue CG mark is behind the spot where my cutout balances on the aluminum angle! In order to make Sounder stable, according to the cutout method, it looks like I'd have to make the front end of the rocket much heavier, to move the CG further forward.

So, what gives? Can the cutout method be said to represent the CP of a rocket at all?

Well, the answer is yes - but only in certain circumstances. We'll talk about that in the next post.

Click here for Part 4.

*Original OpenRocket file by Jim Parsons - a.k.a. K'Tesh. His OpenRocket work can be found on The Rocketry Forum in this thread. It's helpful to have these, because you can take them and tweak them, which is a lot of fun.

Follow me on Twitter.

Like my Facebook page for blog updates and extra stuff.

Have a question you'd like to see addressed on this blog? Email me at iamtherocketn00b@gmail.com.

Repairing and Enhancing the Quest Magnum Sport Loader - Part 4: Fixing the Sim Part B

Click here for Part 1

In the last post, we removed all the Center of Gravity (CG) and mass or weight overrides on the simulation of our rocket.

Now we have to find the CG and total weight of the actual model, so we can get a more accurate simulation to use. This will help us figure out what motors we want to use the in the rocket on a given launch day, so that we can reach a maximum altitude on nice calm days, and keep the altitude lower on windier days, to lessen the chance we'll lose our awesome rocket.

An accurate simulation will also tell us how long a delay grain we need for those motors. For example, do you want to use C6-3 (3-second delay), C6-5 (5-seconds) or C6-7 (7 seconds) motors? The difference is important.

Even though I've been focusing these posts on my particular rocket - the Quest Magnum Sport Loader, which I recently had to shorten to cut off some damage - these principles can be applied to any model rocket.

We'll need the following things for this last step:

• The rocket, including the recovery system (parachute, streamer, etc.)
• A length of string, or something on which to balance the rocket, such as the back of a chair
• A digital scale
• Recovery wadding
• A tape measure
• A pencil or pieces of masking tape to mark locations on the rocket

You'll also need your OpenRocket or Rocksim simulation open on your computer.

Once we've found the true weight of the built rocket, and the true CG, we will override those elements in our simulation. Then we'll get an accurate representation not only of its caliber of stability, but we'll be able to run flight simulations with a reasonable degree of accuracy, which will aid us in picking the right motors for a particular flight.

First, we'll weigh the rocket to find the true mass or weight of the finished model. Our simulation says the rocket weighs 101 grams without motors. That is the sum of all the parts in the OpenRocket design file. OpenRocket will insert these automatically when you build a design file. It takes an assumed density for a particular material - say, balsa fins - and will calculate a mass or weight based on the part's dimensions.

In reality, the density and weight of items like balsa fins and other parts will vary. Fins, especially, will vary in density and final weight. There are dense balsa woods and soft, lightweight balsa woods, and different rocket kits will have different qualities of balsa. Even the weight of the individual fins in a single kit will vary slightly.

But even if all the parts in our design file were accurate, OpenRocket doesn't take a couple of important things in rocket construction into account - glue and paint. Those things do add mass, and will change the final weight of the built rocket.

So, to get an accurate simulation, we do need a digital scale. It doesn't have to be fancy or expensive - a decent digital kitchen scale will do. And even though I'm working with the metric system here, you can also work with the Imperial scale (pounds and ounces) if you happen to have a scale which uses that system. The main thing is that the scale be accurate and sensitive enough to detect small changes in mass.

I have two digital scales, and they both work really well. Both of them were very reasonably priced.

The scale above left is a small metric scale which can measure to an accuracy of 0.1 gram. That's very sensitive, and perfect for small rockets and parts. It has a maximum capacity of 600 grams, a little over 1.3 pound. It cost less than $10 on Amazon.com.

The scale to the right can weigh in Imperial units, detecting pounds, ounces and tenths of ounces, or in metric units, accurate down to a single gram. It has a capacity of 110 pounds and a larger plate, meaning it can be used for larger rockets - which is great when you graduate to building and flying high power rockets. And it was only about $25 on Amazon. I was surprised to find such a good scale for such a reasonable price!

Since I'm going for maximum accuracy and working with a small enough rocket, I'm going to use the small metric scale.

What we need to find is the weight of the rocket itself, without the motors. Once we add motors to our simulation, the weight in OpenRocket will change, as will the CG, as we will see below.

You do need the parachute installed in the rocket, and, though it might surprise you, you should also install the recovery wadding. Why, you might ask? Aren't we trying to find the empty weight of the rocket?

Well, yes. But when running simulations, OpenRocket also doesn't take recovery wadding into account. You will always fly with the stuff (unless you are using a rocket with an ejection baffle, a device permanently installed in the rocket which protects the recovery system from the heat of injection charges), so you should assume it's part of the simulation.

Recovery wadding doesn't weigh much, so if you forget to install it, it probably won't make a big difference. But, for accuracy's sake, it's a best practice to consider wadding a part of the recovery system, and weigh it with the rocket.

Turn on the scale, let it boot up, and when it reads "0.0," carefully place the rocket on the scale.

The Magnum Sport Loader weighs 106.6 grams. The simulation of the rocket states that it's 101 grams. That's pretty close. Does that mean that the glue and spray paint on this rocket weigh 6.6 grams? Hard to say, since I didn't weigh the individual parts of the rocket as I was building it, as I tend to do now.

At any rate, I need to change the weight of the rocket in the simulation, so we'll turn to our design in OpenRocket.

Up near the top left of the screen, in the design elements window, select Stage.

Double-click on Stage, or press the Edit button to the right. The following dialog box will pop up.

Check the Override mass box, and type in the weight of your rocket.

And now, as I write this, I learn something new: OpenRocket will not allow me to enter a mass of 106.6 grams. It rounds up to 107 grams. If I were to enter 106.4g, it would round down. So it's accurate to within a half a gram, but no closer. This will do just fine.

Now that we have an accurate weight for the rocket, it's time to find the true Center of Gravity. You can leave the Stage configuration dialog box open for now.

A quick and easy way to find the approximate CG for your rocket is to balance it on your finger. That's fine for flying out in the field - say, if you're trying a new, heavier motor and you just want to make sure the CG doesn't move too far back when you install it in the rocket. But I want to mark the CG on the rocket, so I'm going to balance mine. You can use the back of a chair or some other sturdy object with a straight thin edge. But I found it helpful to use a loop of string.

Here, I have the rocket balanced on the tube cutting jig you saw in Part 1 of this series.

Problem is, it took me a lot of adjusting the rocket back and forth by tiny increments to get it to balance like this, and it tried to roll off. Then, when I went to mark the CG, it fell off the jig.

With a loop of string, the rocket won't roll around, and once you find the CG, you can keep the string in the same spot on the rocket until you grab a pencil or piece of tape to mark the spot.

Make a simple loop in the string - here, I'm using a piece of Kevlar shock cord - and slip it over the rocket. Again, you need everything installed in the rocket except the motors. This includes the parachute and recovery wadding.

Find the spot where the rocket balances.

This is the CG of your unloaded rocket. You can mark the spot with a pencil or piece of tape. Since I didn't want to put a pencil mark on the paint, used low-tack painter's tape.

I grab the loop of Kevlar string to hold it in place on the rocket...

...and carefully line a piece of tape up with the Kevlar. The nose cone is to the left of the frame
of this picture, so the leading edge of the tape represents the CG of the unloaded rocket.

Now that we have the CG marked on the rocket airframe, how do we measure its position?

CG and CP are measured as a distance from the tip of the nose cone. You might just grab a cloth tape measure and place it at the tip of the rocket and then measure from there.

But this is a little like measuring your height by placing a tape measure on top of your head, and measuring around the curvature of your head down to the ground - it's going to make you seem taller than you actually are. If you measure along the curvature of the nose cone, you're going to get a false measurement.

You need to measure straight back. The way I do this is by placing the nose cone against a flat, vertical surface, such as a wall, and measuring from there back to the place.

Here, I have the rocket sitting on a cradle, to keep it horizontal to the table, and placed against a metal file box.

Then, I place the tip of a metal tape measure flush against the metal box and measure straight back to my CG mark on the rocket. As mentioned in a previous post, I always switch to the metric system when doing measurements like this, because it's simpler - everything is divisible by 10.

The CG of my rocket is 29cm (or 290mm) from the tip of the nose cone.

For comparison's sake, here's the measurement I got by measuring along the curvature of the nose cone with the cloth tape measure:

The blue tape is holding the tape measure in place just so I can take a picture.

With this method, I get a CG location of 29.5cm - a half centimeter difference.

Is this a big deal? Will it make much difference? Am I being too fussy here?

Well, maybe it won't make much difference how you measure the CG and CP locations on many rockets. But for the simulation, I'm trying to be as accurate as I can. And if you're measuring the rocket to check its stability margin, you want to measure as accurately as possible. Remember that the minimum margin of stability is 1 caliber - the diameter of the rocket itself. The CG needs to be forward of the CP by at least 1 caliber. If you have a rocket which is right at that 1-caliber margin, you want to make sure you get a good measurement. It might make the difference between having to add weight to the nose cone or not.

Alright, so we have our real-life CG location - 29cm, in my case. Let's put that into the sim. Go back to the Stage configuration dialog box in OpenRocket. Click the check box marked Override center of gravity, and input the actual CG location.

Now the blue and white CG symbol on the rocket design will move. In the case of the Magnum Sport Loader, it moves from here:

To here:

The bulk of the work is now completed. We just have a few more minor details to adjust, then we can run some simulations.

Click here for Part 5

Like my Facebook page for blog updates and extra stuff!

Follow me on Twitter @rocketn00b.

Repairing and Enhancing the Quest Magnum Sport Loader - Part 3: Fixing the Sim Part A

The shortened simulation of the rocket shows stability to be marginal - only 0.627 caliber. Below, we fix that.

Click here for Part 1

This is kind of an addendum to the previous two posts on repairing the Quest Magnum Sport Loader and then verifying its flightworthiness. The actual model is finished, stable, and ready to fly. Now, I want to fix the simulation in OpenRocket to reflect the actual model.

Why do I want to do this? A couple of reasons. The first is curiosity: I want to see how accurate OpenRocket is in finding the correct Center of Gravity (CG) when I load different motors. Sometimes I look at the CG on a RockSim or OpenRocket file, and wonder can that really be right?

But more importantly, I want to be able to run flight simulations before I actually go out to launch the rocket. Depending on weather conditions - wind, mainly - I might decide to put different motors in the rocket. On a particularly breezy day, a high flight increases the likelihood that I will lose one of the models I'm proudest of. And if I fly an altimeter in the payload compartment, that could be an expensive loss. Running a flight simulation will give me a rough idea of how high the rocket will fly with different motors. I can then make a more informed decision whether to put A, B or C motors into the rocket, depending on how high I am willing to let the rocket fly on launch day.

I can then also compare the simulation to the data from actual flights, recorded on the altimeter. I can see how close to the predicted altitude the rocket actually flew. Then I can look back at the simulation and figure out how I might make the predicted altitude more accurate. That's part of what makes rocketry interesting. There's more to it than just watching something go up and come down.

I think I should mention that as good as rocket simulators are, they're almost never 100% accurate when it comes to altitude prediction. There are just too many variables to account for in the physical flying environment. But they're pretty good, and much better than guessing. And, as I said before, I'm not a master at OpenRocket, but I know enough for a beginner to be reasonably accurate.

Let's get started.

First thing, I start OpenRocket, and open the original RockSim file, downloaded from the Apogee Components website. This is what I see.

This original design file has not been altered to reflect the shorter, repaired rocket. Before I do any of that, I'm going to "Save as" an OpenRocket file. OpenRocket and RockSim are mostly compatible, but not 100%. Sometimes, if you make a change to a RockSim file in OpenRocket, then save all your changes and close the file, you will find when you go back to the file, some of the changes you made have not been saved. Saving the file as an OpenRocket (.ork) file will fix this problem.

Up in the design box, we see a number of things we'll want to change.

Every weight symbol means that the mass, or weight, of something has been overridden. Every blue and white circle (the CG symbol) means that the CG of something has been changed. These are on several components, but in fact they don't matter as much as the overrides on the part called Stage. That refers to the entire rocket (or to the upper stage, if this were a two-stage rocket). Overriding the mass and CG on Stage overrides everything else below it.

We're going to get rid of all the overridden data for this simulation and input our own.

The rocket's mass has been overridden in the simulation. With no motors, it is said to weigh 99.2 grams.

When you remove part of a rocket in real life (in this case, we removed nearly 2 inches of the airframe when we repaired the rocket), the mass will change a bit. But in the last post, you saw that simply shortening the airframe in the design file wasn't enough - because the CG had been overridden to 35.6 cm, no matter how much I shorten the tube, the value won't change.

Obviously the Center of Gravity can't be behind the rocket!

That's the same for the mass. In fact, since the override on Stage outranks any other override on any component, I could make each of the fins weigh 20 pounds, and the simulator will still say that the rocket weighs 99.2 grams.

First thing I'll do is remove the mass override for Stage. Double-clicking on Stage on the design components box brings up a dialog box.

Simply remove the check mark in the Override mass box, and the mass of the rocket will equal the combined mass of all the parts.

Suddenly, the rocket is said to have a mass of 281 grams! That's a huge difference.

The CG, however, remains where it is - 35.6cm from the tip of the nose cone. We'll remove that override as well.

Incidentally, you can use either grams or pounds and ounces. I am sticking with grams for now, because I have a digital scale which uses metric and is accurate to 0.1 gram, and I'll use that to complete the simulation here.

Let's get rid of the CG override.

Suddenly, the CG jumps way forward, to 16.9cm from the tip of the nose cone, in the lower third of the payload section.

And here we see why the rocket weighs so much. There are "mass components" in the payload section, representing the payload this rocket is designed to carry - in this case, raw eggs.

Oddly, though the rocket only has a capacity for two eggs, there are three of them represented here. They are called "Egg1," "Egg2," and "Unspecified," but they all seem to represent eggs, because they all weigh about the same - 63 grams.

Two of them are hard to see, because they have been assigned a length of 0 by the person who built this simulation. One of them is located exactly where the nose cone meets the black coupler attaching it to the payload section. You can see it more clearly if I highlight it.

Raw eggs are heavy - about 2 ounces a piece. And three of them won't even fit in this rocket. Besides, we want to get an idea of what the rocket will do with no egg payload at all. If we want to fly one or two eggs, we can add these back to our simulation.

I select each egg in the design elements box and delete them. The CG has now shifted aftward, and the total mass of the rocket is now said to be 98.7 grams.

Now we're getting closer. I'm going to make a few more alterations to the simulation before turning to the physical rocket to take my measurements.

First, I've decided to fly the rocket with only one parachute. The rocket is designed to separate at apogee and come down on two chutes - the payload comes off and descends on its own parachute. I have decided I don't like this for a couple of reasons - I want to keep the parts of the rocket together, and I'm not confident the chute for the rocket booster will always come out of the airframe without the weight of the nose cone pulling on it. So I'm going to delete one of the parachutes, as well as the mass overrides and CG overrides of any components which have them. I'm also adding a shock cord, because the rocket obviously has one, despite the fact that it's not present in the design file. Finally, I'll shorten the airframe to match the repaired rocket I have.

I'll go back to the simulation and override a few things once I've weighed and measured the physical rocket itself. For now, though, I have a simulation file which is of accurate length to match the model I have on hand, with a CG said to be 24.8cm from the tip of the nose, and a mass of 101 grams with no motors installed.

What I need to find out to have a reasonably accurate simulation - and one which will tell me if the rocket is stable - are two things: The actual weight or mass of the completed rocket (with no motors installed) and the actual Center of Gravity of the completed rocket (again, with no motors installed). I can then input that information into the simulation. Finally, I'll find the CG of the rocket with motors installed, and see how accurate the CG in the simulation is with virtual motors installed in the simulation.

We'll do that next time.

Click here for Part 4

Like my Facebook page for blog updates and extra stuff.

Or, follow me on Twitter.